So I was wasting time on reddit the other day (happens all too often) where I came across the following video of a girl practicing spinning for figure skating using an off-ice apparatus:
You can see the post I read here, there were a lot of comments about how spinning that fast can’t possibly be good for the girl’s brain. My initial response was that since her head is at the center of the axis of rotation there really isn’t any force on it, but technically that’s not true: if you have something soft and squishy and you spin it really fast, it will bulge out in the middle and compress slightly at the top and bottom along the axis of rotation:
Note: thanks to thingiverse for the brain model, and blender for the rendering.
It probably doesn’t stretch out this much. But can we estimate how much it actually does stretch out when someone’s head is spinning around this fast? How would we estimate this? There are three pieces of information we need:
- How fast the girl is spinning
- Physical parameters of the brain
- A model or equation to calculate/estimate the deformation of the brain while its spinning
Speed of Spinning Girl
How can we figure out how quickly the girl is spinning? This should be fairly straightforward with some video analysis. Analyzing the video the way we need to though, requires us to be able to scan the video one frame at a time, and have a timestamp for each frame. Then we can start at the point in the video where the skater is spinning the fastest, walk through several rotations, and count the time elapsed by comparing timestamps. Then the rotation speed is simply # of rotations / time elapsed.
I don’t have any expensive video editing/analysis software, but a quick google search for a free open source software for basic video editing led me to Avidemux.
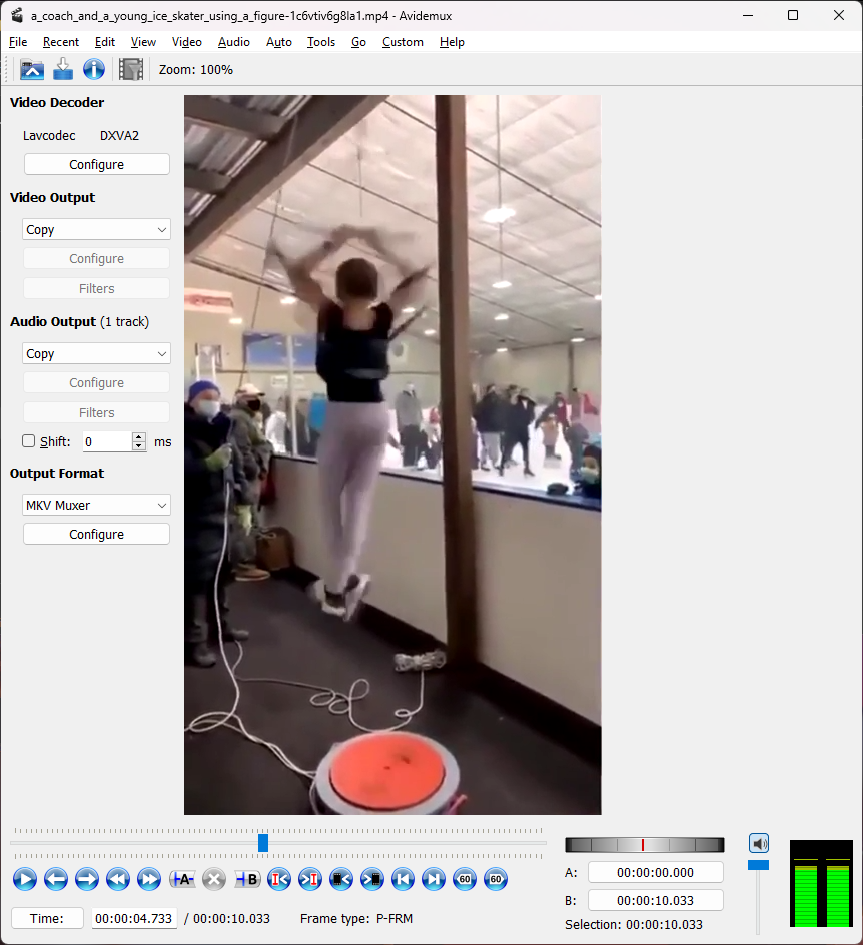
The software lets me step through one frame at a time with the Left and Right keys, and gives me a timestamp at the bottom. More than sufficient for my needs. Starting at 4.733s and ending at 7.833s, she goes through 14 rotations. That comes out to 4.52 revolutions/s.
Mechanical Properties of the Brain
Doing a quick google search for the mechanical properties of the brain almost gave me too much information, there were hundreds of academic papers discussing it. I ended up using this paper: Biomechanical Modeling of Brain Soft Tissues for Medical Applications. It gives values across a range of values from other studies, but I ended up going with a lower-end value (since that will give a larger deformation) of Young’s modulus E = 2 kPa, and Poisson’s ratio of ν = 0.45. For density we’ll just assume it’s about the same as water, since it’s soft tissue and our body is after all mostly water, so that’s a density of 1000 kg/m3.
Deformation Model
This was actually a bit harder for me to find. Searching for “deformation of rotating elastic sphere” and other similar search terms got me lots of papers and pages showing how the earth (or some other planet) bulges at the center due to its spin. However in that case the restoring force trying to return it back to being spherical is gravity, while in our case for the spinning brain it’s simply the object’s own elasticity.
Eventually I was able to find an online solid mechanics textbook that had the derivation for the elastic deformation of a spinning circular plate. Sure, it’s not quite the same as a sphere, but for our intents and purposes we can approximate the brain as a cylinder as much as we can a sphere. For the displacement of the cylinder/disc it gives the following equation:
$$\mathbf{u}=(1-\nu) \frac{\rho \omega^2}{8E} \{ (3+\nu)a^2 r – (1+\nu)r^3 \}\mathbf{e}_r – \nu \frac{\rho \omega^2 z}{8E} \{ 2(3+\nu)a^2 – (3\nu +2)r^2 \}\mathbf{e}_z$$
That’s given in vector form, so since we’re only interested in deformation in the r direction at at the very edge where \(r=a\), we can simplify it to the following:
$$u_r(a) = \frac{\rho \omega^2 a^3}{4E} (1-\nu)(3-\nu)$$
The only parameter we’re missing is the radius of our cylinder. A quick google search tells me that the average human brain has a volume of 1400cm3. If we approximate the brain as a cylinder with equal height and diameter, we can calculate the radius using the following derivation:
$$V = \pi r^2 h = \pi r^2 (2r) = 2 \pi r^3$$
$$r = \left( \frac{V}{2 \pi} \right)^{1/3} = \left( \frac{1400 \text{cm}^3}{2 \pi} \right)^{1/3} = 6.0 \text{cm}$$
We also need to convert our rotation speed to radians/s, which is just multiplying rotations/s by \(2 \pi\) which gives us \(\omega = 28.38 \text{/s}\).
So our final calculation is:
$$u_r(a) = \frac{(1000 \text{kg}/\text{m}^3) (28.38 \text{/s})^2 (0.06 \text{m})^3}{4 (2000 \text{Pa})} (1-0.45)(3-0.45)=0.03 \text{m} = 3.0 \text{cm}$$
Well, that is a very large displacement, our brain is stretching from a 12cm diameter to 18cm! Now there are some problems that this result indicates:
- Our model assumed a simple perfectly elastic solid. In reality this assumption only holds for small deformations, after a certain amount of displacement it ceases to be elastic (i.e. if you relieve the stress then it returns to its original shape) and becomes plastic deformation (i.e. the shape permanently changes), etc.
- The brain is encased in the cranial cavity, and doesn’t have very much room to stretch. The gap between the brain and the cranium is 0.4mm to 7mm depending on the location.
Now if the maximum displacement had been < 0.1mm or so (which is what I assumed) it wouldn’t really make a difference, those assumptions would have been fine. But with this kind of a predicted large displacement we can’t use such a simplified model any more.
But wait! Maybe it isn’t the model itself that’s bad, but the boundary conditions! When solving for the equation for \(u_r(a)\) above, we make the assumption that the radial stress is zero at \(r=a\). However if the brain is constrained inside the cranial cavity so that it can’t expand, then a better boundary condition would be that the displacement \(u_r(a)=0\). This won’t give us much (if any) displacement inside the brain, but we can still calculate the stress inside the brain material.
Redoing the derivation, we start with our differential equation:
$$\frac{\partial}{\partial r}\left( \frac{1}{r} \frac{\partial}{\partial r} (ru) \right)=-\frac{1-\nu^2}{E}\rho \omega^2 r$$
Integrating twice gives us the displacement $u$ with the integration constants \(A\) and \(B\):
$$u=-\frac{1-\nu^2}{8E}\rho \omega^2 r^3 + Ar + \frac{B}{r}$$
The solution has to be finite at \(r=0\), so that means \(B=0\). To solve for \(A\) we set the condition that the displacement has to zero at the edge, or \(u(a)=0\). That gives us a formula for the displacement:
$$u(r)=\frac{1-\nu^2}{8E}\rho \omega^2 (a^2 r-r^3)$$
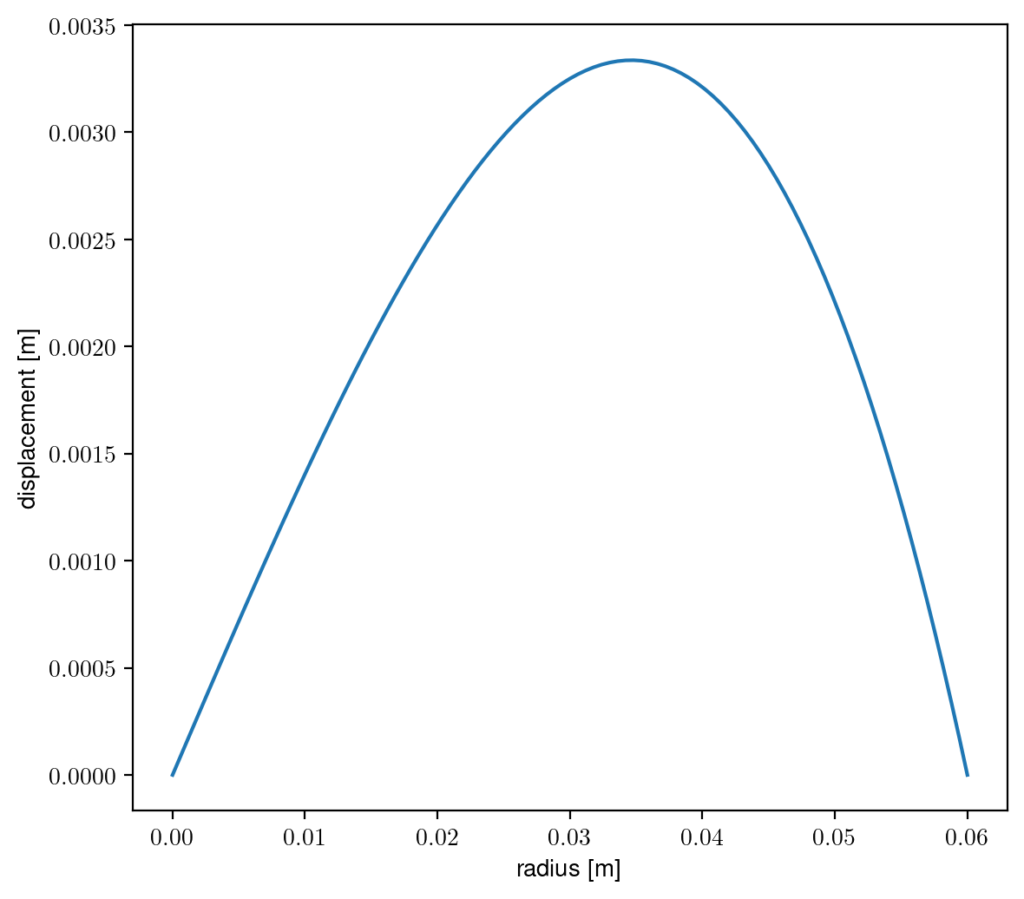
So our cylinder model of a brain is displacing a maximum of about 3mm around halfway between the center and the edge. A more general dimensionless version of the plot is here:
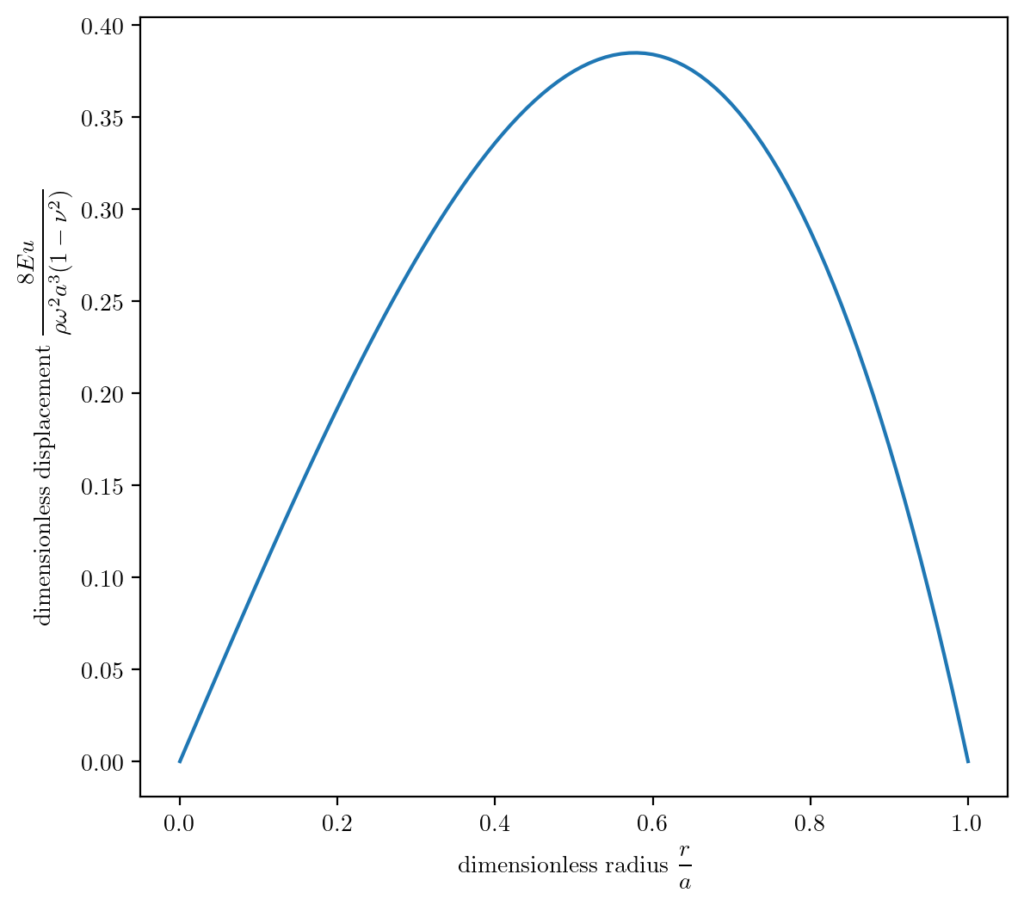
This is a more general version of the solution which is valid for any size cylinder with any known parameters of Young’s modulus \(E\), density \(\rho\), rotation speed \(\omega\), radius \(a\), and Poisson’s radio \(\nu\).
Another thing we can calculate is how much stress there is inside our cylindrical brain as a function of radius.
$$\sigma_{rr}=\frac{E}{1-\nu^2}\left( \frac{\partial u}{\partial r} + \nu \frac{u}{r} \right)$$
Substituting in our derived function for \(u\) we can simplify it to the following function:
$$\sigma_{rr}=\frac{\rho \omega^2}{8}\left( a^2(1+\nu) – r^2(3+\nu) \right)$$
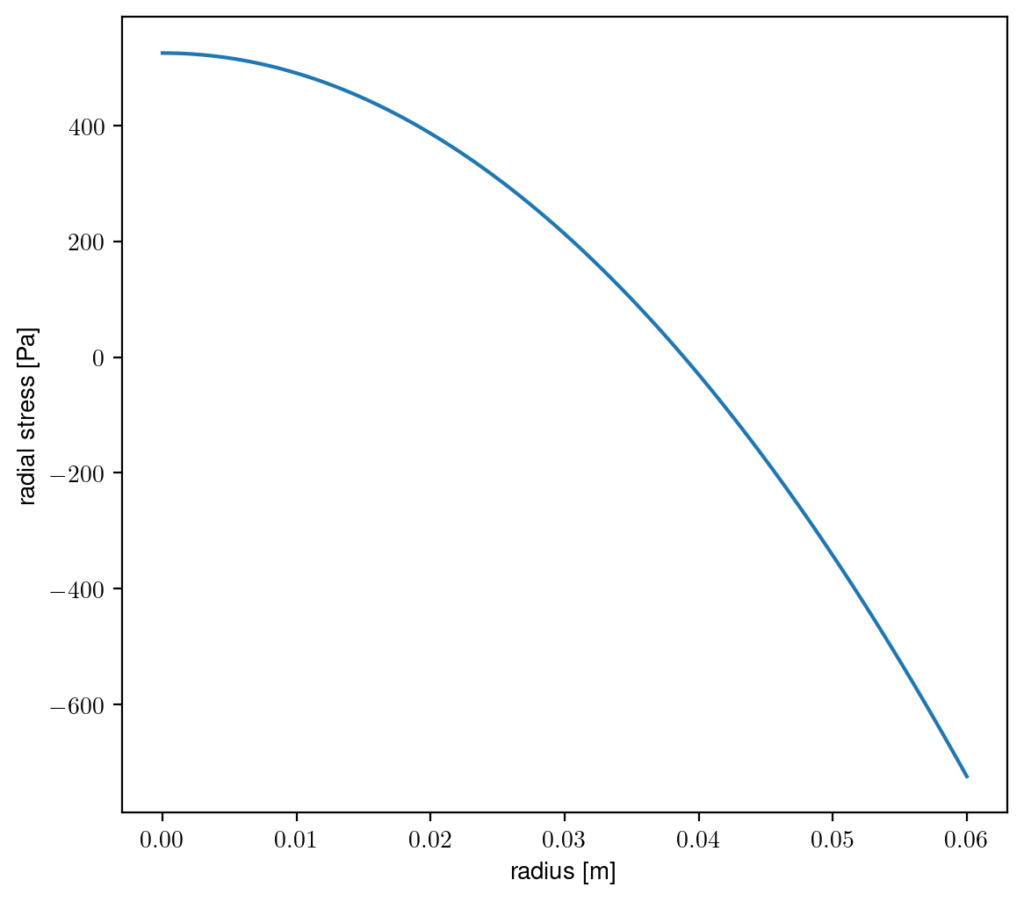
This shows that the ‘brain’ is stretching in the center (positive stress), and being compressed at the edge (negative stress).
I tried to look up how much mechanical stress a human brain can withstand, but it’s almost impossible to filter out psychological stress from search results, and everything else is about sudden shocks to the brain: concussions, CTE, etc.
I found a few papers talking about different types of brain injury:
- S. Kleiven, X. Li, A. Eriksson, and N. Lynøe, “Does High-Magnitude Centripetal Force and Abrupt Shift in Tangential Acceleration Explain High Risk of Subdural Hemorrhage?,” Neurotrauma Reports, vol. 3, no. 1, pp. 248–249, Jan. 2022, doi: 10.1089/neur.2022.0025.
- B. D. Stemper et al., “Head Rotational Acceleration Characteristics Influence Behavioral and Diffusion Tensor Imaging Outcomes Following Concussion,” Ann Biomed Eng, vol. 43, no. 5, pp. 1071–1088, May 2015, doi: 10.1007/s10439-014-1171-9.
- S. Kleiven, “Why Most Traumatic Brain Injuries are Not Caused by Linear Acceleration but Skull Fractures are,” Frontiers in Bioengineering and Biotechnology, vol. 1, 2013, Accessed: Mar. 05, 2023. [Online]. Available: https://www.frontiersin.org/articles/10.3389/fbioe.2013.00015
The second one is specifically related to rapid rotational acceleration, as opposed to impacts which is what almost everything else is. But it’s specifically about acceleration, where in our video the girl isn’t really accelerating that quickly in her rotational motion, even if her rotational velocity is quite high.
So ultimately a bit inconclusive in this post, though I was able to learn a lot about solid mechanics and deformation.